
This article is one part of a longer deep dive into Leios, Cardano’s proposed consensus upgrade. The full post is available at https://314pool.com/post/leios. We’ve broken it into smaller, standalone reads to make it more accessible for the Cardano Cube audience.
In order to understand Leios, it will be important to ensure we’re on the same page with regard to the basic operating principles, important properties, and key scaling limits, of the current network consensus protocol, Ouroboros Praos (or just Praos, for short).
When you submit a transaction, you submit it, either directly yourself or through some public API like blockfrost, to a Cardano node. This node validates that it is correct, inserts it into its own “mempool” (a list of transactions ready to be included in a block), and then shares it with each node it is connected to. Each of those nodes validates the transaction, inserts it into its mempool, and then propagates it downstream to their peers. Through this process, a transaction is “gossiped” around the network. In practice, a given transaction reaches nearly every node in just a few seconds. This means that, while you can’t assume this, in practice every stake pool node has a high degree of overlap in the transactions contained in their mempool.
Every second, each stake pool participates in a “slot lottery” to decide whether it is allowed to produce a new block. Conceptually, they combine some global entropy decided at the start of the current epoch, the slot number, and their VRF private key, to produce a verifiably random number. If that number is below a certain threshold, determined by the amount of stake they had at the start of the previous epoch, then the block they produce for that slot would be accepted by the network.
The threshold needed to produce a block is tuned, such that on average, one in every 20 slots, some stake pool on the network produces a block. Of the 3000 stake pools, roughly 1000 of them produce at least one block each epoch on average. This is referred to as a “Poisson Schedule” because the number of blocks produced in a given window of time follows a Poisson distribution.
The network parameters can be tuned in the following ways:
- More or fewer pools, on average, can be eligible each epoch (the so-called “k” factor)
- On average, there is a higher or lower fraction of slots that produce a block (meaning blocks are produced more frequently)
- The duration of a slot can be adjusted up or down
This process has the important property that nobody but the stake pool operator knows ahead of time when they will produce a block. This means that a clever attacker cannot time an attack on that node to bring it offline at the critical moment. Executing a denial of service on a single server is relatively easy and cheap while executing a denial of service on thousands of potential nodes is prohibitively expensive. So by keeping the block schedule secret, we prevent an attack where someone who wants to do Cardano harm can just direct their bot network to attack each node as their scheduled slot comes up: instead, they have to blanket a large portion of the network, all the time, to have any meaningful chance of appreciably delaying the network.
One of the ways that some other blockchains achieve such high speeds, and a big source of centralization risk, for example, is to have a public leader schedule: when you submit a transaction, you instead send it directly to the next several nodes that are scheduled to produce a block, optimistically assuming one of them will actually produce the block and include your transaction. However, this also means that it would be relatively cheap (on the scale of competitors or small nation-state actors) to consistently and continuously overwhelm those servers as their scheduled block came up.
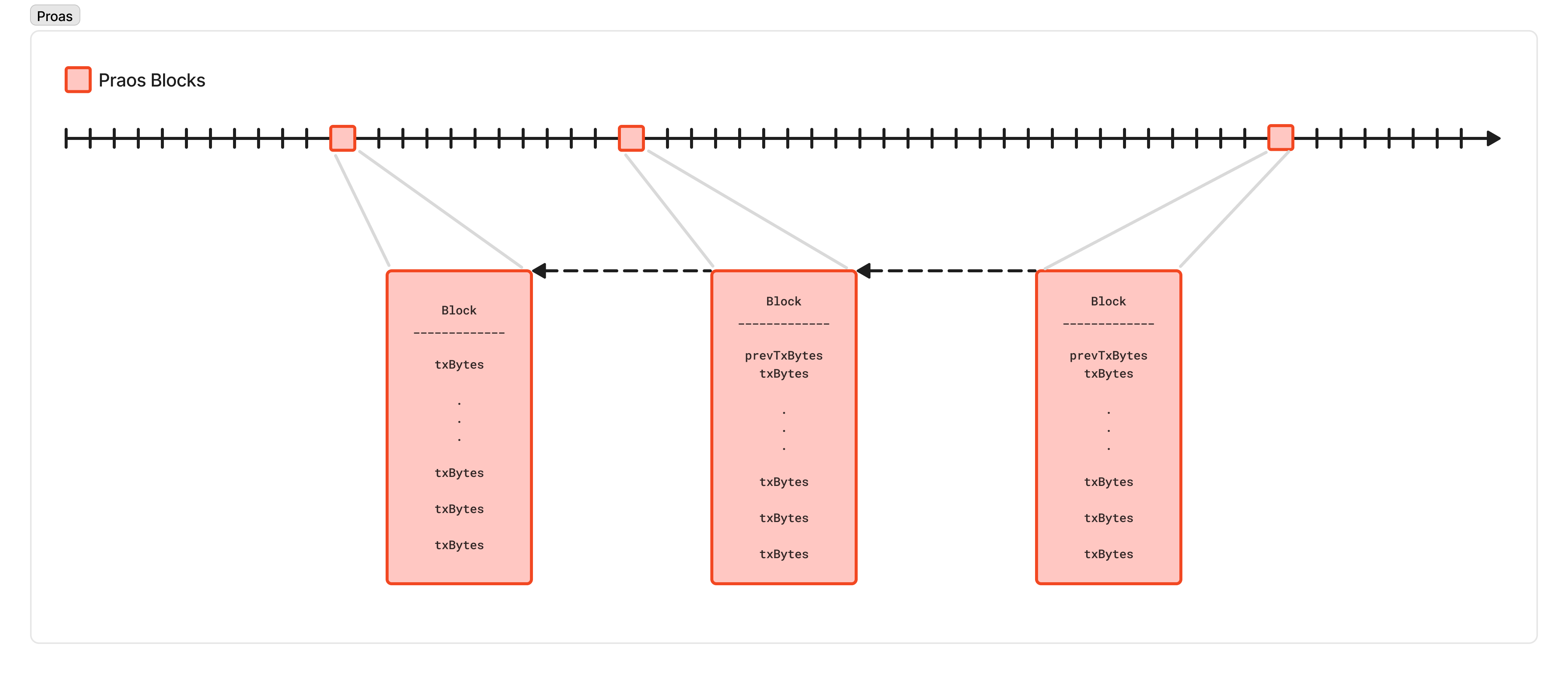
When a node is eligible to produce a block, it grabs as many transactions as it can (up to 88kB worth) from the mempool, produces a block, attaches the proof that they are eligible to produce that block, and begins to gossip that block to its peers in a very similar process to the transaction gossip protocol above.
However, because the schedule is private, and there’s no coordination among nodes to produce a block, there is also no way to prevent two or more nodes from being eligible to produce blocks in the same slot. This is known as a “slot battle” because two nodes are fighting to produce a block for the same slot.
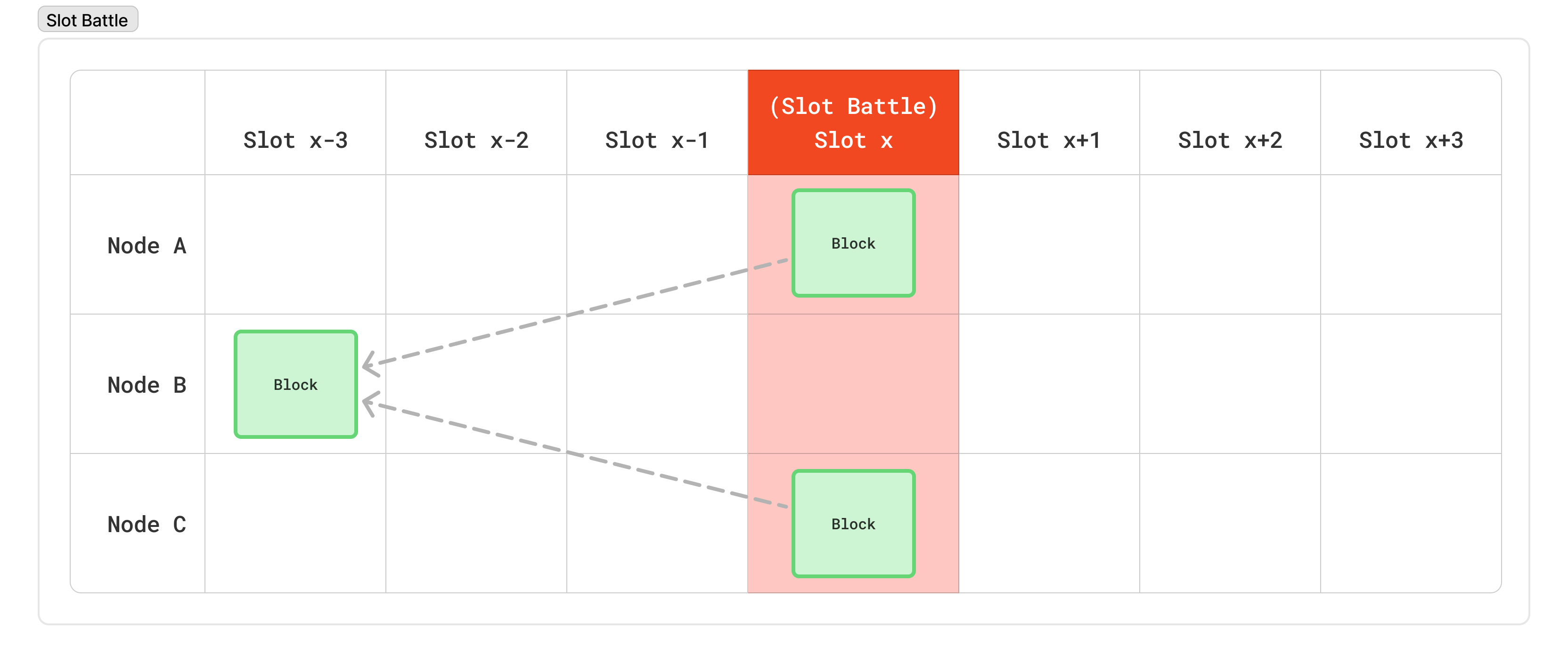
Similarly, because there’s no way to enforce a minimum time between blocks, two different nodes could be eligible to produce blocks back to back. In such cases, it is possible (even likely) that the second node won’t have heard about the previous block’s node. This will lead to two blocks at the same “height”. This is referred to as a “height” battle.
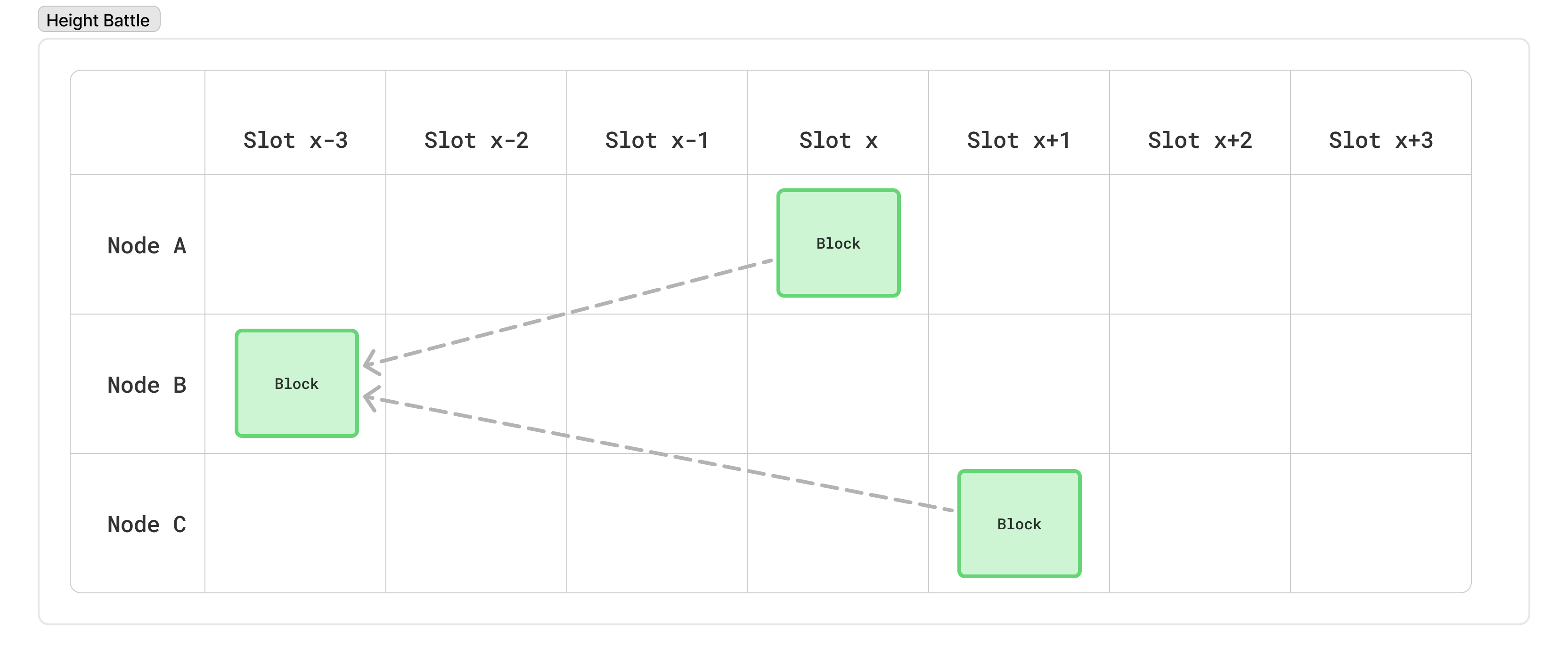
Finally, each of these can be relatively long-lived: there may be a wound in the network that prevents information from propagating efficiently, meaning several blocks could be produced by the time one part of the network learns about another “fork” that, itself, had several blocks produced.
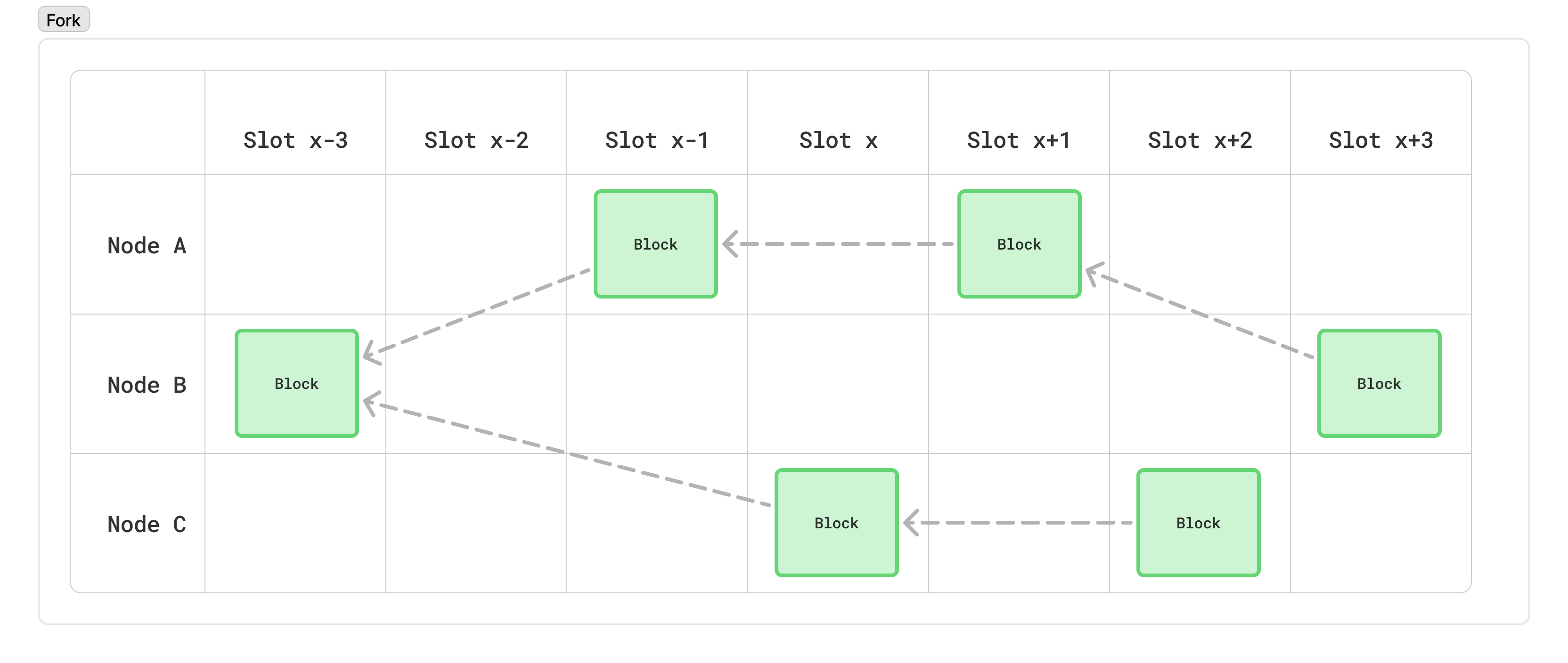
For all of these reasons, the network needs some kind of rule to decide which of these “forks” is valid. In Cardano, a node will always consider the “tip” of the network to be the longest chain of blocks it has seen. This is similar to Bitcoin’s longest-chain rule, so-called “Nakamoto consensus”. This rule ensures it is very difficult for an adversary with a small amount of ADA to create long alternate chains which cause confusion in the network, exactly because there is a low probability that they can create long chains in the first place.
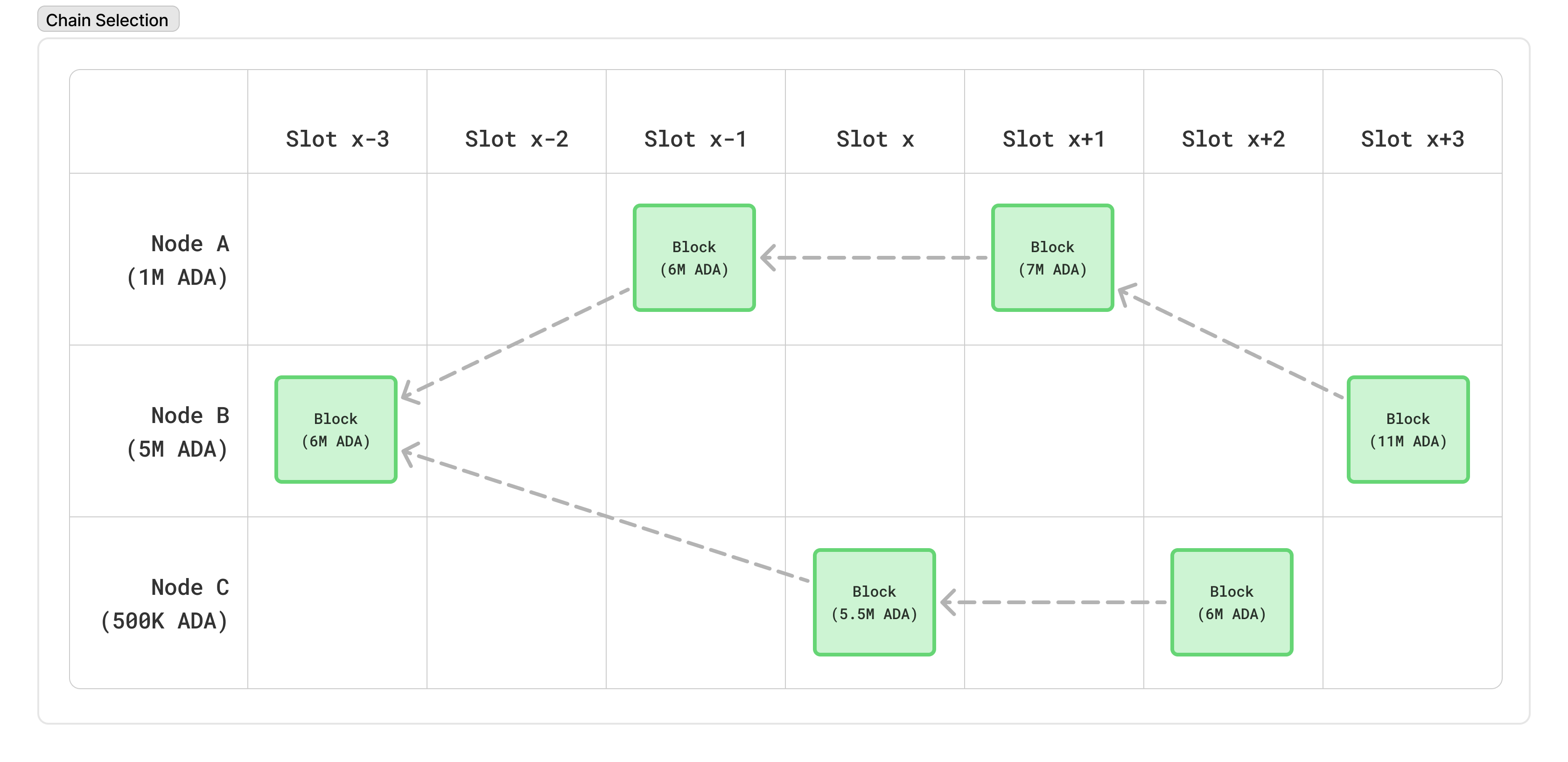
Note: In the above diagram, we assume that Node A and Node C are far enough apart that Node C hasn’t learned about Node A’s blocks by the time it produces its own
The final rule, however, is that a node will never switch to another fork whose common ancestor to the current fork is over 2160 blocks in the past. This is referred to as the “rollback horizon”, and ensures that any block that is at least 2160 blocks old is considered permanent, and prevents an attacker from producing a very long chain in private and revealing it only very late in the game.
All-together, this consensus protocol ensures 2 important properties:
- Everyone converges on the same chain
- The chain continues to grow with honest blocks
Thinking with Light Cones
One framing that will be useful as we study Ouroboros Leios is to think of events in terms of the communication “light cones” on the network. This leans on an analogy to relativistic physics, and is a way to think about the “local view” of a node: all the past events that it can know about, all the future events it can possibly influence, and anything happening “concurrently” that it can do neither.
Consider the diagram below:
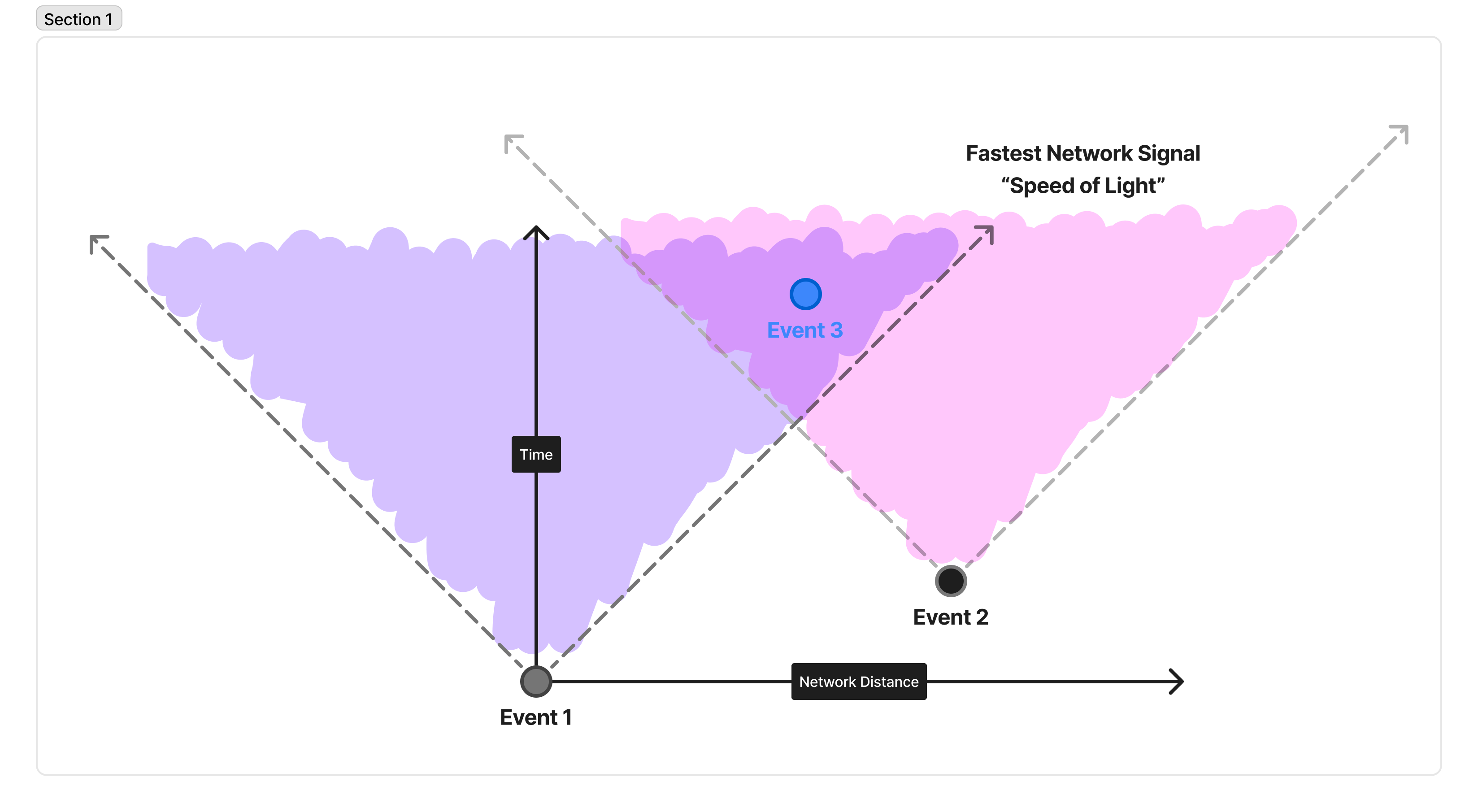
In this diagram, discrete events are represented as circles. They’re separated vertically in time, and horizontally in space. In our case, for example, Event 1 happens, and then Event 2, and then Event 3, because you read from bottom to top. However, Event 2 happened very close to Event 1, and Event 3 happened further away. Here, we don’t mean physical distance, but instead are talking about how fast a network packet could travel from one to the other.
There is fundamentally a maximum speed a message can propagate across the network, represented by the 45-degree angle line. The region inside these two lines is called the “light cone” because it is the cone of all points in space and time that light (a “message” in our example) sent by one event could reach another in time. So, in this example, it is feasible for a message sent by Event 1 to reach Event 3 by the time it happens. Likewise, Event 2 has its own “light cone”, and it’s possible for a message sent by Event 2 to reach Event 3 by the time it happens. However, it is not physically possible for a message sent by Event 1 to reach Event 2 before it happens!
This is why height battles occur: in one second, a node produces a block, but there’s not enough time for that block to reach the next node scheduled to produce a block. Thus, that other node can’t be influenced in any way by the first block, and so they will necessarily fork the chain.
Key scaling limits
So, if we want to scale Praos, what is preventing us from shortening the slot length to 100 milliseconds? Or raising the block density, so we produce blocks every 5 seconds instead of every 20 seconds? Or increasing the maximum size of blocks to 10 megabytes?
Fundamentally, Praos is limited by bandwidth. While short-lived forks are possible (and rather frequent) in Praos, the parameters are selected to ensure that those forks are indeed short-lived. With an average of 20 seconds between blocks, there is plenty of time for each block to propagate across the network and settle disputes about what the canonical tip is.
If you increase the block density significantly, then far more nodes will produce blocks in the same slot, and slot battles will become more frequent.
If you shorten the slot length, then there is much less time between when nodes produce a block. Because of this, height battles become far more frequent.
If you increase the maximum block size, then it takes longer to download the block to be ready to produce the next one, and again, height battles become far more frequent.
The security of the chain degrades as forks become more frequent: with a higher number of forks, you need to increase the rollback horizon to ensure everyone converges on the same chain, meaning transaction finality suffers. Additionally, the honesty guarantees of the chain worsen, and you can have longer stretches between honest blocks, meaning an attacker can start to pick and choose the transactions they include, which can be used to bias the stake distribution in their favor (by, for example, refusing to include any transactions which delegate away from them), or bias the entropy selected for next epoch so they get an abnormally large number of blocks, et cetera.
This security degradation is not linear; It is challenging to say “Well, we set those parameters very conservatively, so maybe it’s ok to accept a 20% reduction in security for 20% more frequent blocks”. Instead, even small reductions in this margin lead to exponentially worse security properties for the chain over long periods of time.
We can see how changing these parameters increases the number of forks fairly intuitively if we look at the light cone behavior of producing a block. Here is the standard, happy path of blocks being produced on Cardano, depicted as a light cone diagram.
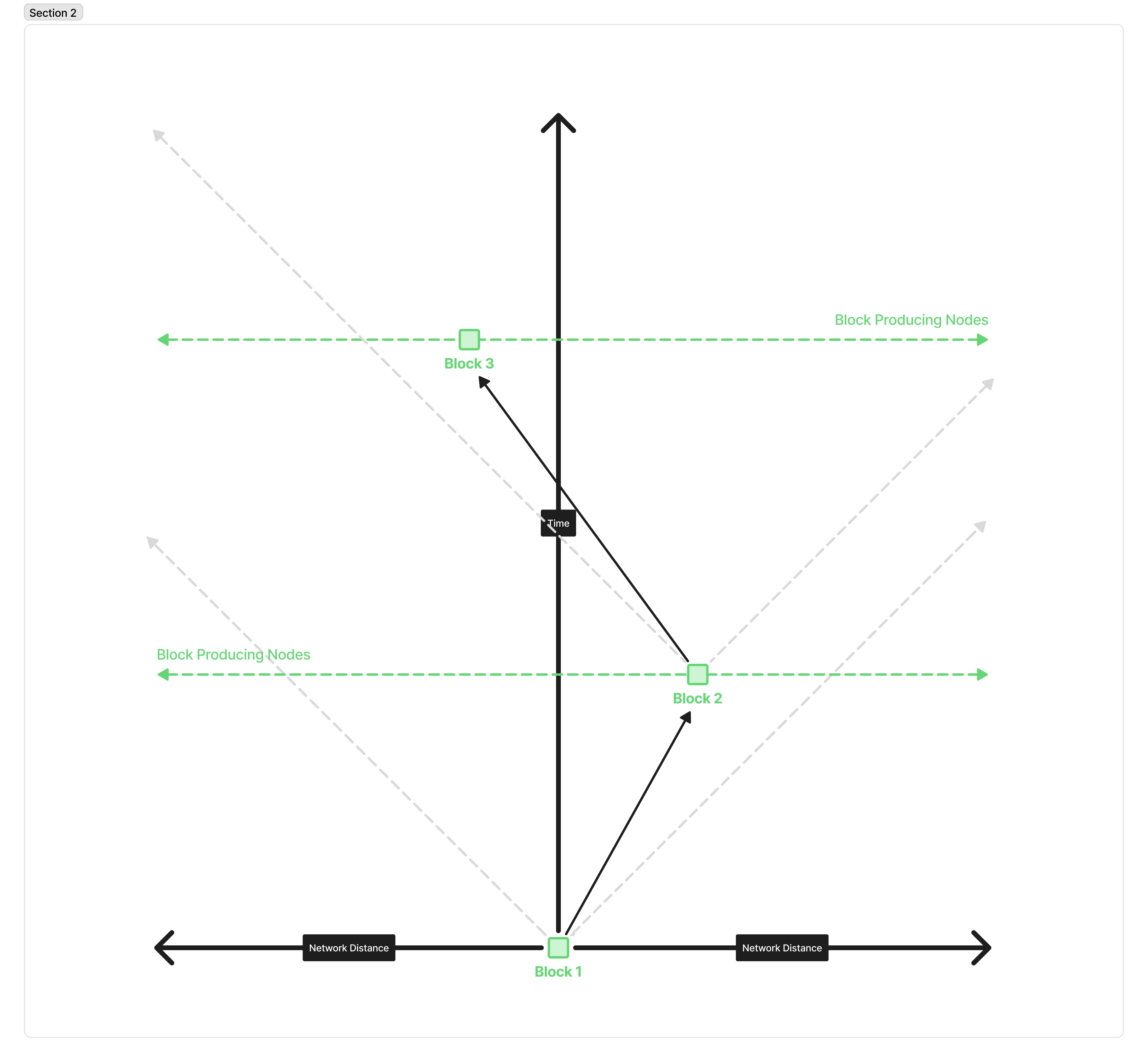
This depicts 3 consecutive blocks being produced, with no slot or height battles. The grey lines represent the fastest the block could travel across the network. The arrows represent (some of the) messages traveling through the network; the circles represent blocks being produced; and the green lines represent all of the various block-producing nodes on the network.
Block one is produced and propagated across the network. Because there’s a decent gap between Block 1 and Block 2, it has plenty of time to reach any node in the network that might happen to produce the next block. The same is true from that new node propagating its block across the network within its own “light cone”.
But, if we compress the time between blocks heavily, the picture starts to look like this:
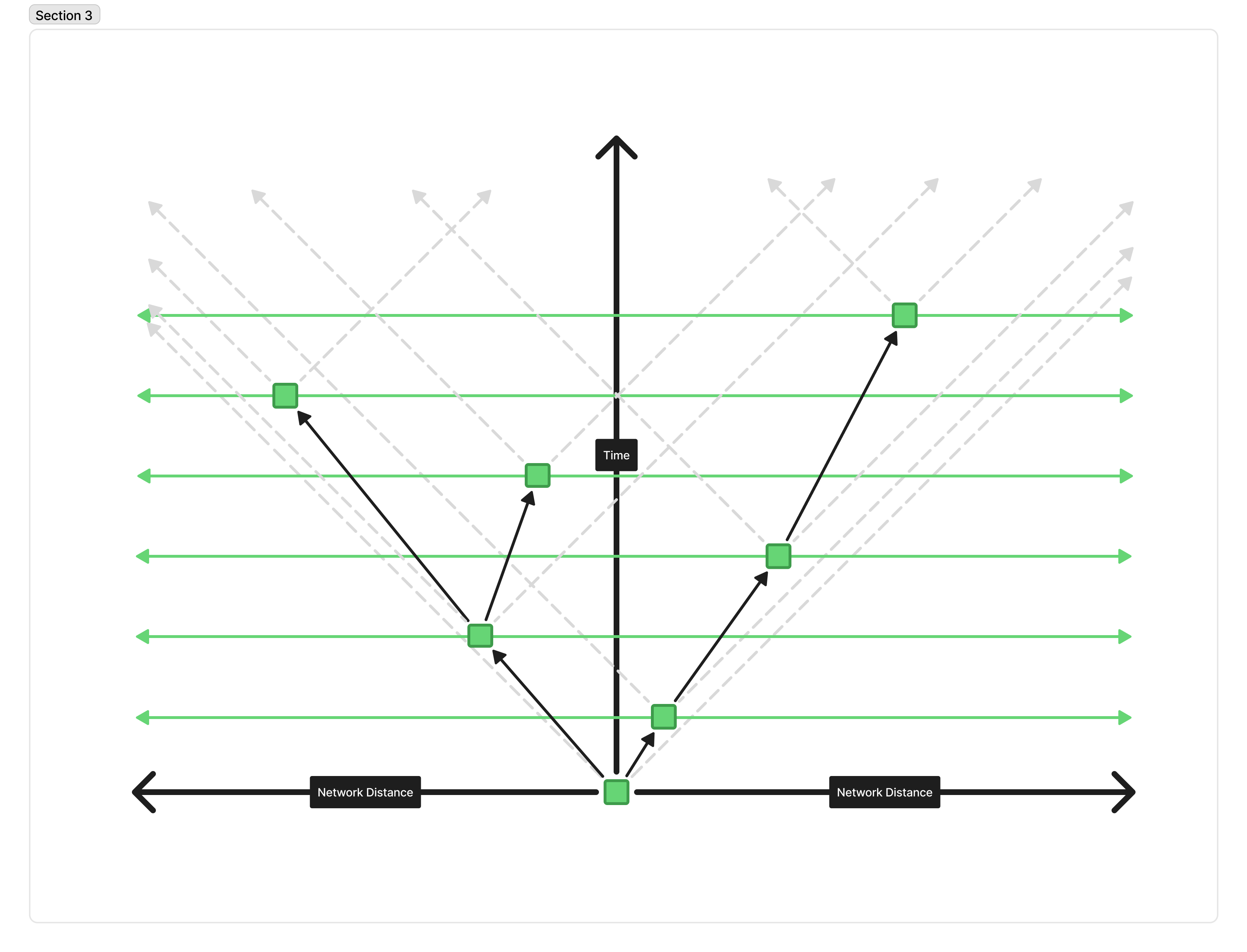
We can see that forks immediately become much more frequent because there is often not enough time for a block to propagate to the next peer that will produce a block.
Similarly, if we make blocks bigger, it takes longer to download these blocks, meaning messages propagate across the network slower, effectively “narrowing” our light cone, and a similar picture emerges:
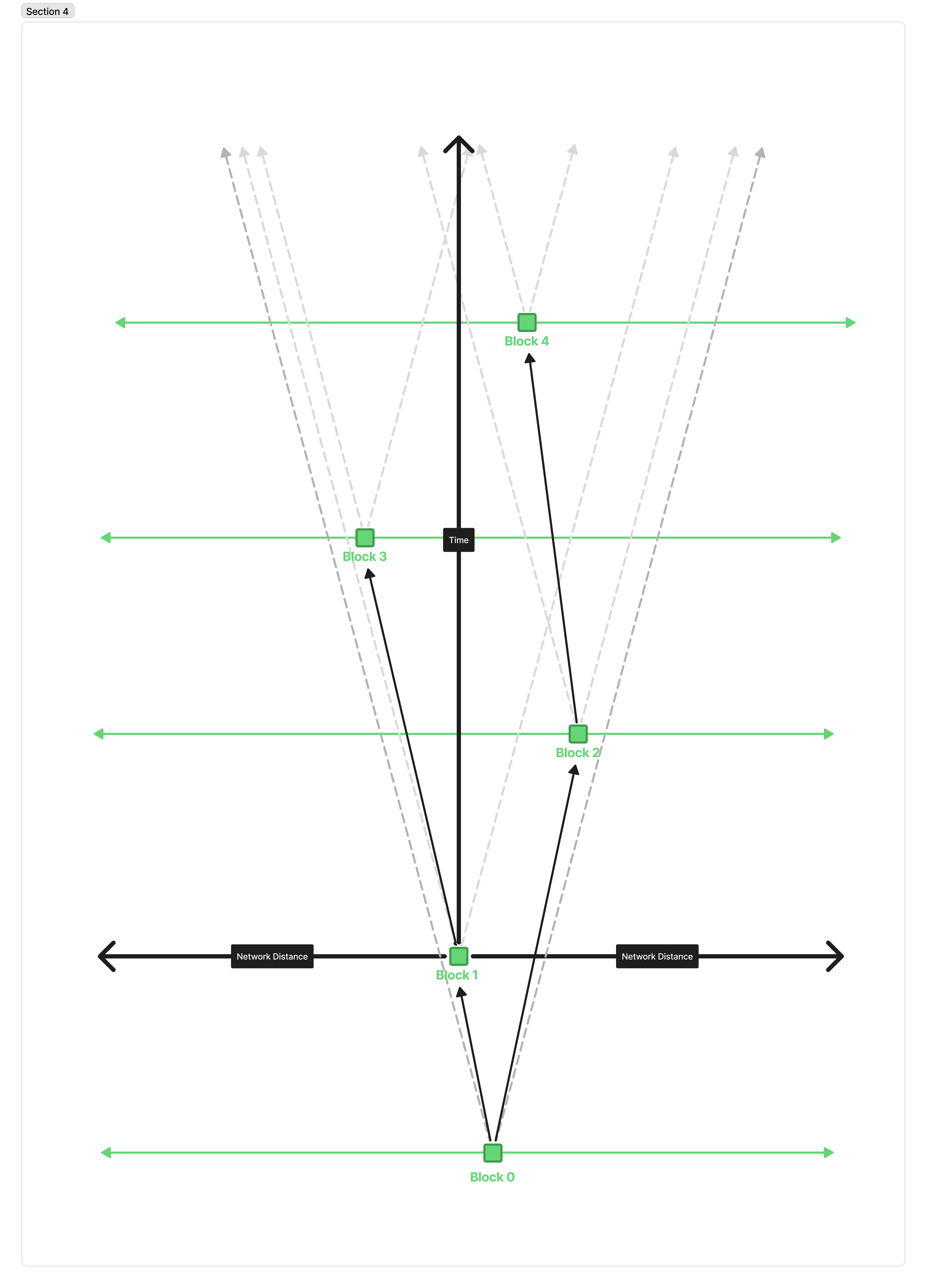
Forks emerge because even though a smaller message could have reached the next node in time, alerting them that it exists, they won’t be able to finish downloading the block, so they can’t validate it to produce the new block on top of it.
So the key takeaway is that Praos relies on a relative “quiet” period between blocks, to ensure that blocks have plenty of time to saturate across the network before the next block gets produced. This quiet period means that there is a fundamental tension between the security and throughput of the network. The throughput of the network is constrained by the worst-case scenario of two blocks being separated by a single second, but the average case only has to process blocks every 20 seconds or longer. In practice, a node spends less than 1% of its time doing useful work!
Two key questions led to the invention of Leios. I leave them here, in case the clever reader wants to ponder on them on their own before reading on to how Ouroboros Leios solves this:
- What if we could produce blocks in parallel, and only sequence them later?
- What if we didn’t have to download the blocks at all to decide on a sequence?
Next up: Building up to Ouroboros Leios